LA TRANSFORMADA DE FOURIER

José María Martínez Ansemil.

Catedrático de análisis matemático y funcional.

El catedrático José María Martínez Ansemil, ha realizado esta prueba de espectro a un alumno empleando la Transformada de Fourier. Si nos fijamos en la fotografía nº1 hay tres armónicos palpables en verde azul y violeta. El azul dará lugar a dos armónicos más e incluso asoma a la derecha de la imagen un armónico en rojo que quiere formarse como consecuencia del estudio del canto.

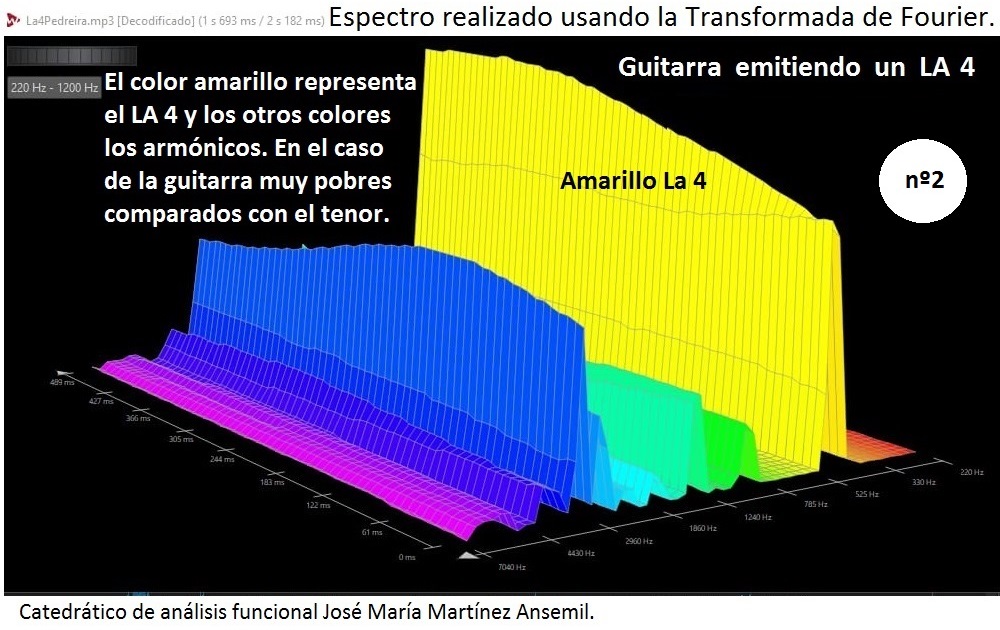
La Transformada de Fourier sirve entre otras muchas cosas para analizar el espectro de la voz de un tenor. El amarillo es el LA4, los otros colores son los armónicos que emite el individuo al que se le hace la prueba. En la fotografía nº2 podemos ver la misma prueba hecha a una guitarra emitiendo un LA4 también, en donde podremos apreciar que en la parte que corresponde a los armónicos es muy pobre

(Material por gentileza de Manuel Pedreira)

Wikipedia dice:

Definición: La transformada de Fourier es básicamente el espectro de frecuencias de una función. Un buen ejemplo de eso es lo que hace el oído humano, ya que recibe una onda auditiva y la transforma en una descomposición en distintas frecuencias (que es lo que finalmente se escucha). El oído humano va percibiendo distintas frecuencias a medida que pasa el tiempo, sin embargo, la transformada de Fourier contiene todas las frecuencias del tiempo durante el cual existió la señal; es decir, en la transformada de Fourier se obtiene un solo espectro de frecuencias para toda la función.

La transformada de Fourier, denominada así por Joseph Fourier, es una transformación matemática empleada para transformar señales entre el dominio del tiempo (o espacial) y el dominio de la frecuencia, que tiene muchas aplicaciones en la física y la ingeniería. Es reversible, siendo capaz de transformarse en cualquiera de los dominios al otro. El propio término se refiere tanto a la operación de transformación como a la función que produce.

En el caso de una función periódica en el tiempo (por ejemplo, un sonido musical continuo pero no necesariamente sinusoidal), la transformada de Fourier se puede simplificar para el cálculo de un conjunto discreto de amplitudes complejas, llamado coeficientes de las series de Fourier. Ellos representan el espectro de frecuencia de la señal del dominio-tiempo original.

La transformada de Fourier así definida goza de una serie de propiedades de continuidad que garantizan que puede extenderse a espacios de funciones mayores e incluso a espacios de funciones generalizadas.

Sus aplicaciones son muchas, en áreas de la ciencia e ingeniería como la física, la teoría de los números, la combinatoria, el procesamiento de señales (electrónica), la teoría de la probabilidad, la estadística, la óptica, la propagación de ondas y otras áreas. En procesamiento de señales la transformada de Fourier suele considerarse como la descomposición de una señal en componentes de frecuencias diferentes, es decir, {\displaystyle g}G corresponde al espectro de frecuencias de la señal F{\displaystyle f}. La rama de la matemática que estudia la transformada de Fourier y sus generalizaciones es denominada análisis armónico.

Toda la información en Wikipedia:

https://es.wikipedia.org/wiki/Transformada_de_Fourier